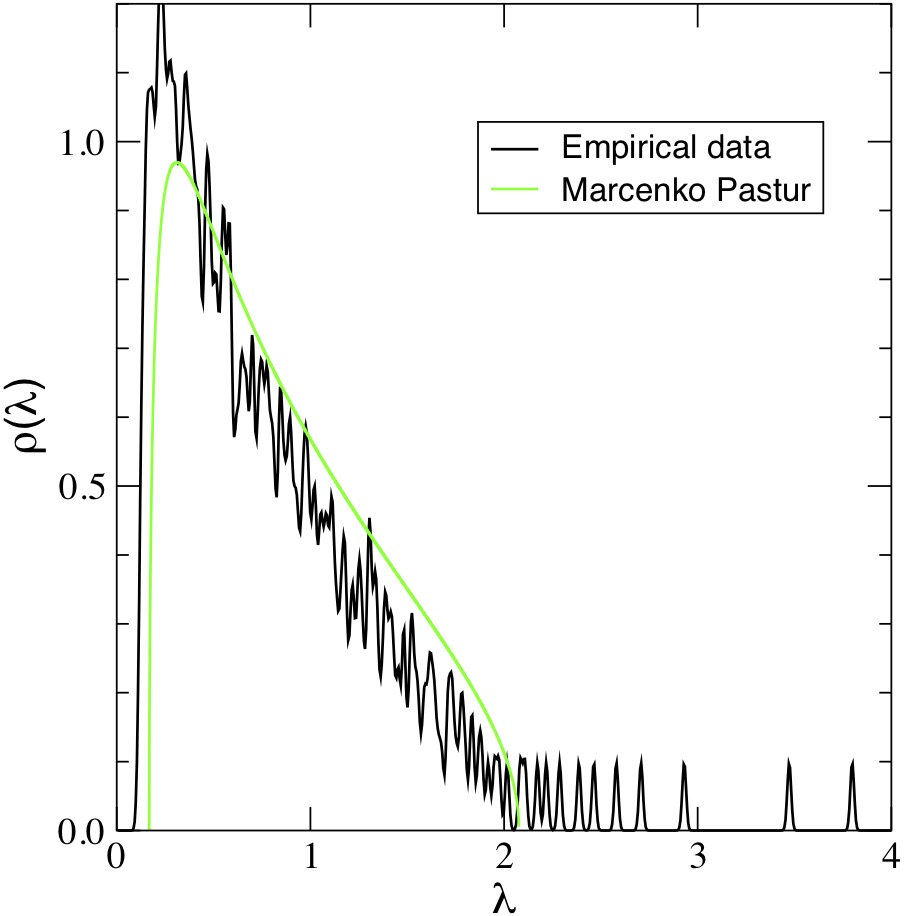
Random Matrix Theory (the study of the asymptotic properties of large matrices) is a growing field of research with applications in physics, finance, telecommunication, computational biology and data science. It provides an accurate descriptive model of the noise in random symmetric (Hermitian) matrices (semi-circle law) and sample covariance matrices (Marcenko-Pastur distribution).
The course will introduce students to the tools used to study the properties of eigenvalues and corresponding eigenvectors. Fundamental results such as the semi-circle law and Marcenko-Pastur distribution will be derived many times using different techniques. The goal of the course will be to understand the recent results in estimation of large noisy matrices and in particular of sample covariance matrices.
This course will focus on getting computationally useful results for large matrices found in real applications. The level of rigor will be that of physics.